「数学って、社会で何の役に立つの？」そんな声をよく耳にします。でも、実は高校で習う三角関数は、社会の様々な場面で活躍しています。

tan関数

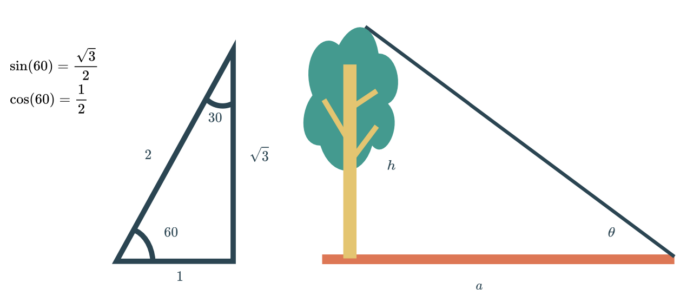
たとえば、測量の世界ではその力が発揮されます。ある木の高さを直接測れないときでも、三角関数を使えば簡単に計算できるのです。

例題2-14-1

木からの距離が a メートル、木のてっぺんを見上げたときの角度が θ 度だった場合、
次の式で高さ h を求められます：h = a × tan(θ)

角度はラジアンに変換する必要があります（JavaScriptの Math.tan はラジアン角を使うため）。

次のコードを実行して木の高さを計算してみよう。

function setup() {
  const a = 20; // 木までの距離 (m)
  const t = 32; // 角度 (度)

  // 角度をラジアンに変換
  const t_rad = (t * Math.PI) / 180;

  // 高さを計算 (tan を使用)
  const h = Math.tan(t_rad) * a;

  console.log(`木の高さ: ${h.toFixed(2)} m`);
}

📌 三角関数を使った別の活用事例

sin関数・cos関数

ゲームのキャラクターが円を描くように動いたり、時計の針を回したり、視点を回転させたりするときにも、三角関数は欠かせません。
特に sin や cos は 円運動の表現に不可欠です。

三角関数を使えば、中心が原点(0,0)、半径 r の円周上で、角度 θ の位置にある点の (x, y) 座標を以下のように求められます：

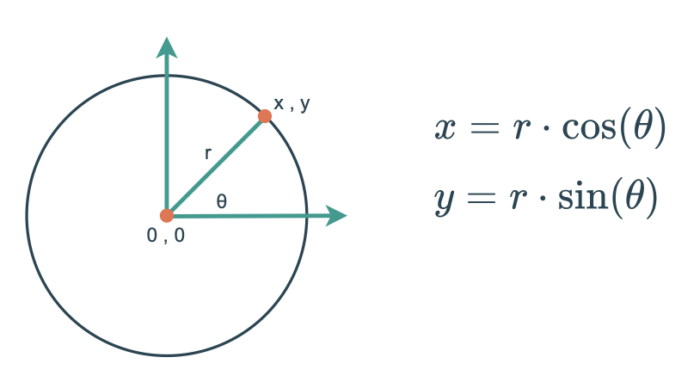
例題2-14-2 〜練習問題

sin関数・cos関数を使って正５角形を描いてみましょう。

先ほどの木の高さを求めるときに使ったtan関数と同様に三角関数で指定する角度はラジアン（弧度法）である必要がありますが、人間には分かりづらいです。また、いちいち角度をラジアンに変換するのは面倒です。そこでangleMode(DEGREES)を使うことによって、三角関数をラジアン（弧度法ではなく、馴染みのある度数法で指定することができるようになります。下記の例題で確認してみて下さい。

function setup() {
  createCanvas(400, 400);
  background(255);
  
  translate(width / 2, height / 2);
  scale(1, -1);

  noStroke();
  fill(255, 200, 200);

  angleMode(DEGREES);
  const r = 80;

  // 正５角形を描く
  let x;
  let y;
  let angle;
  
  angle = 0;
  x = r * cos(angle);
  y = r * sin(angle);
  circle(x, y, 10);

  angle = 72;
  x = R * cos(angle);
  y = R * sin(angle);
  circle(x, y, 10);

  // 残りの3点を自分で描いてみよう！
}

練習問題2-14-2a

上記の正５角形を描くプログラムをfor文を使って短くまとめなさい。

練習問題2-14-2b

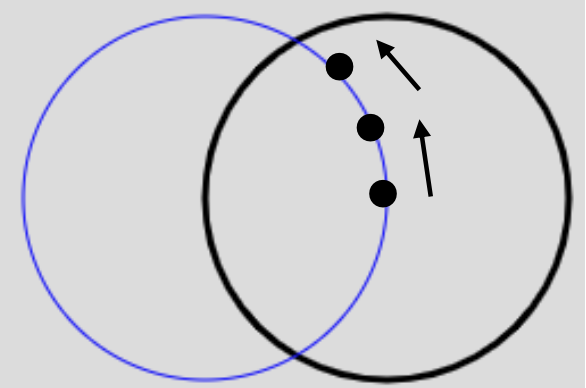
青の円の円周上の点を中心に同じ半径の黒の円を描く。
これを角度をずらしながら、円周上を一周する。
すると次のような図形が描ける。

【問題】

円の円周上の点を中心に同じ大きさの円を描きながら、円周を一周するプログラムを作成してください。

下記のひな型をコピーして作り始めなさい。なお、原点はキャンバスの中央に移動されています。

【条件】

半径80 の円周上に 36個 の点を取り、それぞれの点を中心に半径 80 の円を描く。
座標計算には三角関数 cos, sin を使用すること。
円は枠線のみ（塗りつぶしなし）で描くこと。

function setup() {
  createCanvas(400, 400);
  background(220);
  
  // 原点をキャンバスの中央に移動
  translate(width / 2, height / 2);
  
  // Y軸を反転（上がプラス、下がマイナスになる）
  scale(1, -1);

  // 度数法を使用
  
  // 円を描く

}

練習問題2-14-2c

円周上で 120°の角度を成す2点を直線で結ぶ。始点 x1,y1 の円周上の位置は 5°ずつ反時計方向に回転させてできる図形を描きなさい。円の半径は150とする。

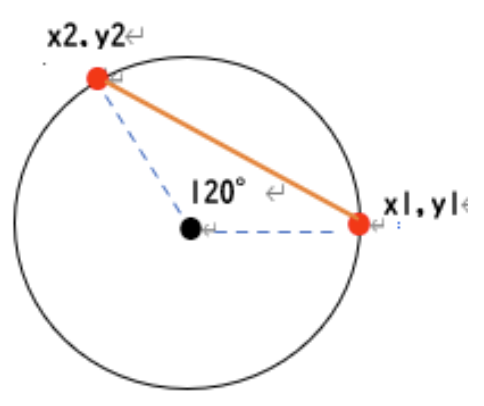
この表の結果から、グラフ表示する場合のx座標とy座標の範囲を考えなさい。キャンバスのサイズは 400×400 とする。

結果

例題2-14-3

円周上を16分割した各点を総当たりで結ぶ。このとき描かれる図形をダイアモンドリングと呼ぶ。総当たりといっても、すでに描いた直線は引かないので、最初のくり返しで15本、次のくり返しで14本・・・と一本ずつ少なくなる。

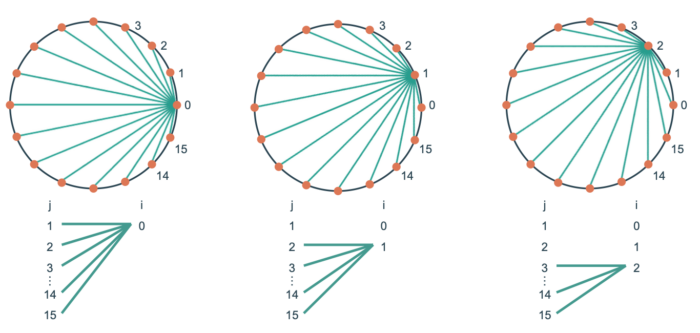
次のコードを実行してどのような図形が描かれるか、確認ししてみよう。

コード

function setup() {
  createCanvas(400, 400);
  background(220);
  
  // 原点をキャンバスの中央に移動
  translate(width / 2, height / 2);
  
  // Y軸を反転（上がプラス、下がマイナスになる）
  scale(1, -1);
  
  // 度数法を使用
  angleMode(DEGREES);

  // 分割数
  const N = 16;  

  // 円の半径
  const radius = 150;
  
  for (let i = 0; i < N; i++) {
    let x1 = radius * cos(i * 360 / N);
    let y1 = radius * sin(i * 360 / N);
    
    for (let j = i + 1; j < N; j++) {
        let x2 = radius * cos(j * 360 / N);
        let y2 = radius * sin(j * 360 / N);
        line(x1, y1, x2, y2);
    }
  }
}

結果

練習問題2-14-3

例題のプログラムを改造して、カラフルにしたり、自由にアート作品を作りなさい。完成したら、先生にスクショをSlackで送りなさい。