三角関数まとめ

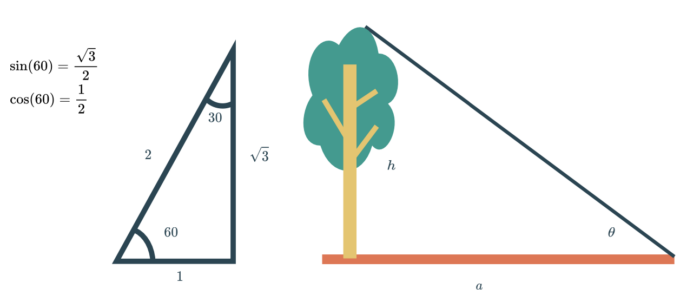
　最初は角度（ｈ）を求めるのにcos. sin.使うことが難しかった。　　　　　　　　　　　　　　　　　　

　けれど、下の図のような表し方だと、とてもわかりやすく感じられた。

　初めにやった問題では、ダイヤモンドリーグを活用した問題だった。

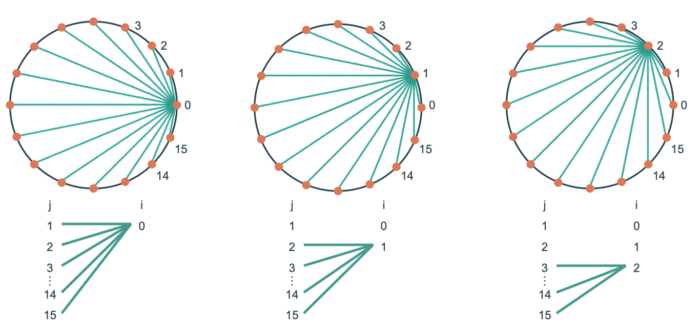
　そこから例題として下の図のようなデザインを書いた。

　　けど、先生が作ってくれた「座標の（０. ０）の場所を移動するコード」を追加してくれたおかげで、なんとか問題を解くことができた。

　　実際の問題とアレンジ⇓

function setup() {
  createCanvas(400, 400);
  background(220);
  
  // 原点をキャンバスの中央に移動
  translate(width / 2, height / 2);
  
  // Y軸を反転（上がプラス、下がマイナスになる）
  scale(1, -1);
  
  // 分割数
  const N = 36;  

  // 円の半径
  const radius = 150;
  
  // 度数をラジアンに変換するための定数
  const RADIAN = Math.PI / 180;
  
//   for (let i = 0; i < N; i++) {
//     let x1 = radius * Math.cos((i * 360 / N) * RADIAN);
//     let y1 = radius * Math.sin((i * 360 / N) * RADIAN);
    
//     for (let j = i + 1; j < N + 1; j++) {
//         let x2 = radius * Math.cos((j * 360 / N) * RADIAN);
//         let y2 = radius * Math.sin((j * 360 / N) * RADIAN);
        
//         line(x1, y1, x2, y2);
//     }
//   }
  // z = 0;
  // for (let i = 0; i < N; i++) {
  //   let x1 = radius * Math.cos((0 + z) * RADIAN);
  //   let y1 = radius * Math.sin((0 + z) * RADIAN);
  //   let x2 = radius * Math.cos((120 + z) * RADIAN);
  //   let y2 = radius * Math.sin((120 + z) * RADIAN);
  //   line(x1, y1, x2, y2);    
  //   z += 5;
  // }
  noFill();
  //ellipse(-50, 0, 150, 150);
  z = 0;
  for (let i = 0; i < N; i++) {
    let x1 = 80 * Math.cos((0 + z) * RADIAN);
    let y1 = 80 * Math.sin((0 + z) * RADIAN);
    //let x2 = 100 * Math.cos((0 + z) * RADIAN);
    //let y2 = 100 * Math.sin((0 + z) * RADIAN);
    
    //circle(x1, y1, 160);
    // random(0, 255);
    stroke(random(0, 255), random(0, 255), random(0, 255));
    ellipse(x1, y1, 160, 160);
    z += 10;
  }
}

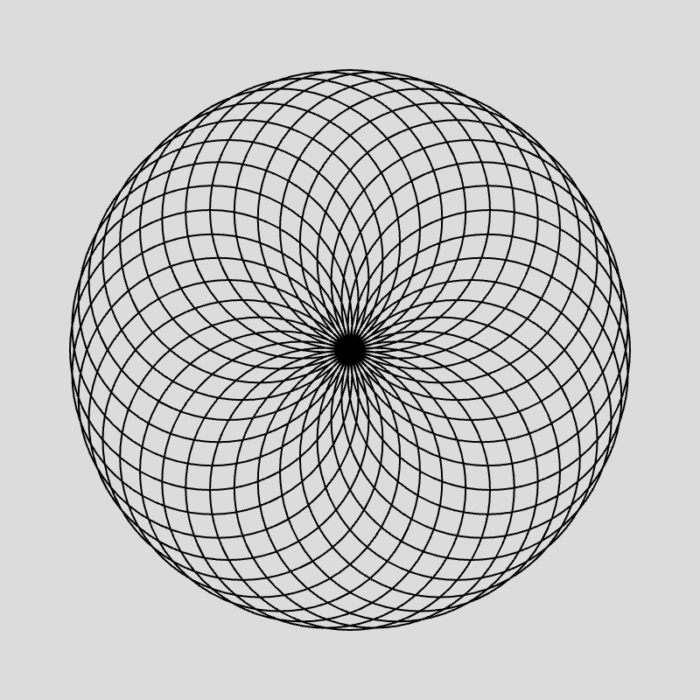
　　⇑このデザインをアートっぽく変えてみた

　　三角関数の威力を学んでみて、とある場所の座標を求めてそこから形を作るところが　楽しく、細かいようなデザインをこれからも自分で書いてみたいと思うようになった。

　　三角関数の威力を活用して、現代の芸術をより新しくできるのではないかと自分は思った。

コメントする コメントをキャンセル

コメントするコメントをキャンセル