目次
学習日
2025年11月25日
名前
樋口桜大
はじめる前に・・・
前回学習した「比例のグラフ」の書き方を使って、今回は「反比例のグラフ」を描いてみよう!
比例と同じように「反比例」も日常の中に色々あります。
- 時間 = 距離 ÷ 速度 → 同じ距離を異なる速度で移動するときの時間
- 密度 = 重さ ÷ 体積 → 同じ重さの物体の密度
- 単価 = 金額 ÷ 数量 → 同じ金額で買える商品の単価
- 効率 = 仕事量 ÷ 時間 → 同じ仕事量をこなすときの効率 などがあります。
今回も以下の特徴を確認したうえでグラフを描いてみよう。
– 原点(0, 0)を通らない双曲線
– x軸とy軸に近づくが交わらない(漸近線)
– a が正なら第1象限と第3象限、a が負なら第2象限と第4象限
自分で作った図形(コードと画像)
✅ 練習問題 20-3-1
前回学んだ点描画法を使って、反比例のグラフを描いてみましょう。 比例と同じように、1本のforループで左から右まで点を打つ方法でやってみよう!
・y = 1 / x
📷 実行結果
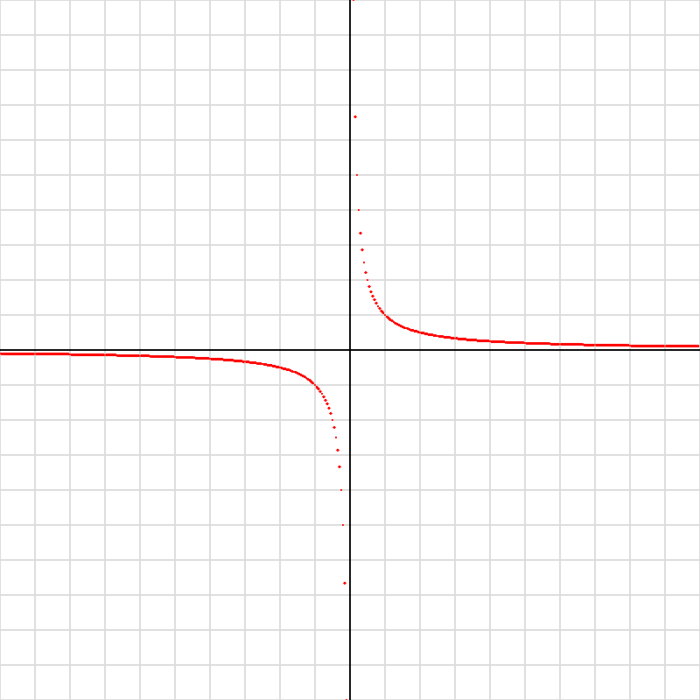
✅ 練習問題 20-3-2
ゼロ除算について
反比例 y = 1/x では、x = 0 のときに y = 1/0 となり、数学的には定義できません! しかし、プログラムではなぜエラーにならなかったのでしょう?
デバックして確かめてみよう。
📷 実行結果
7.646661082105766e-15, 130776032736711.31xが完全にゼロにならず、非常に小さな値になっているからこのような数値になります。
なんだろうこの数字…?e-15とか意味わからなくなってくるー!
10進数で1/3 = 0.333…と終わりなく続いてピッタリ書けないのと同じように、コンピューターが裏で扱っている2進数では0.05がピッタリ書けません。xに0.05を足し続けると、その「書ききれない分」のズレが少しずつたまって、本当は0になるはずの場所でもxは0ではなく、ごく小さな数になります。それによって1/xはエラーではなく、とても大きな数として計算されます。 xの値が0になると、1/xはInfinity(無限大)になります。
✅ 練習問題 20-3-3
x = 0 に近い値を避けて、安全に反比例のグラフを描く方法を考えてみましょう。
x の絶対値が 0.01 より大きい場合のみ描画するように条件分岐を追加してみよう!
📷 実行結果
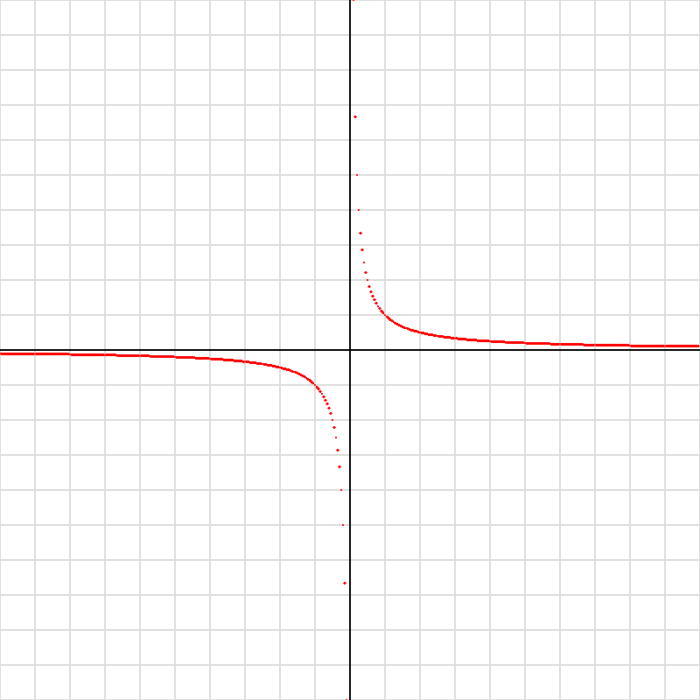
✅ 練習問題 20-3-4
点描画では原点付近が粗くなってしまいます。 手書きで曲線を描くように、カーブを描く命令(curveVertex)で点と点の間を補完してみよう。
curveVertex
curveVertex(x, y)は複数呼び出し座標を指定することにより、その座標を滑らかな曲線で結んでくれる命令です。命令を使う前にbeginShape()で開始を宣言し、最後の点を指定したらendShape()で終了を宣言しないといけません。
📷 実行結果
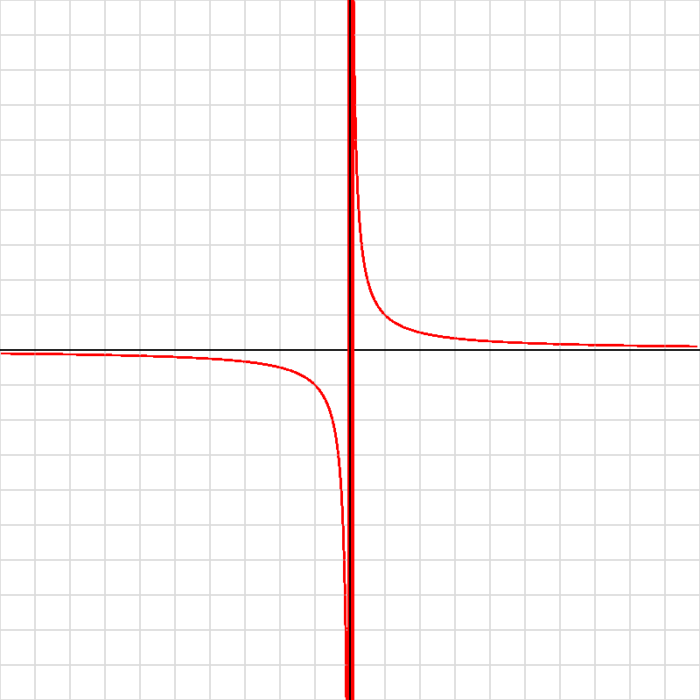
✅ 練習問題 20-3-5
なぜ、グラフがおかしなことになっている理由を考えてみよう。
理由・・・xがゼロに近い値になった時に、yが急激に増えることでその間も結んでしまっているから。
✅ 練習問題 20-3-6
原因を解決するには、Y軸付近では描画をしないようにする必要があります。 endShape() と beginShape() を使って、グラフを分離しよう!
📷 実行結果
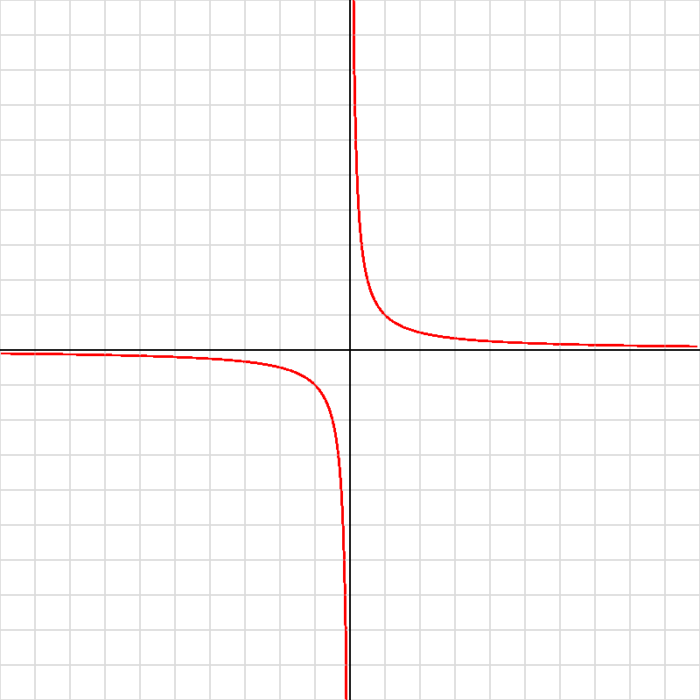
ポイント
- for文「1つ」で0に近い値を避けるように命令する。
- beginShape()とendShape()の使うタイミングを条件判定で工夫する。
- console.log()を使って、xの値を出して数値を示すのも一つの手だよ!
✅ 練習問題 20-3-7
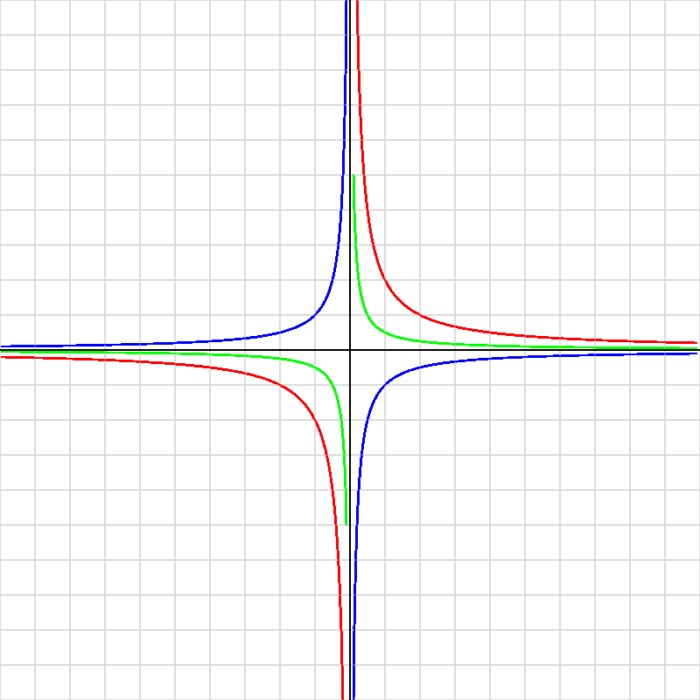
y = 1/x の係数を変えて、グラフの形がどう変わるか確認してみよう!
- y = 2/x を描く(より急な曲線)…赤色
- y = -1/x を描く(第2象限と第4象限)…青色
- y = 0.5/x を描く(より緩やかな曲線)…緑色
📷 実行結果
✅ 練習問題 20-3-8
for文のステップを0.05に細かくしましたが、0.01や0.001にすればもっと細かくなるのか・・・? 実験する前に考えてみよう。
理由・・・0.05の時点で、直線のように見えているため、これ以上細かく打っても見え方は変わらないから。
まとめ・感想
・今回初めて使った「beginShape()」と「endShape()」を条件判定の中で使う時に、どの判定の時に終わらせるのかなどを工夫して命令するのが難しかった。
・反比例のグラフでは、比例のグラフと大きく違っていた「Infinityを避けること」の時に、「console.log()」を使うことで、簡単にxの値を割り出すことができた。
・グラフを書く時に打った点についても、前回の比例のグラフ同様に、どれだけ細かくしても、直線には変わりないということがわかった。