目次
学習日
2025年10月14日
名前
樋口桜大
まず、はじめに・・・
・みんなの身近な生活の中には、「比例」は様々なところに存在しています。
– 距離 = 速度 × 時間 → 一定の速度で移動するときの距離
– 金額 = 単価 × 数量 → 同じ値段の商品を複数買うときの合計金額
– 重さ = 密度 × 体積 → 同じ材質の物体の重さ
– 給料 = 時給 × 働いた時間 → アルバイトの給料計算 など色々あります。
そんな中学の数学で習った「比例」をグラフを使って描いてみましょう。
以下の特徴をおさらいしたうえで描いてみよう。
グラフの特徴:
– 必ず原点(0, 0)を通る直線
– a の値が大きいほど傾きが急になる
– a が正なら右上がり、a が負なら右下がり
自分で作った図形(コードと画像)
✅ 練習問題 20-2-1
数学で習ったように、ある2点を定規で結ぶというやり方は、プログラムでも近場の2点を結んだ後に延長するという手法は実現が難しいです。 どうしてでしょう?
理由・・・p5.jsでは、線を引く(line)という命令があります。この命令は2つの場所を示し、その間を結ぶというものなので、プログラムでは引くのが少し難しいです・・・。
✅ 練習問題 20-2-2
20-2-1の理由から、y = 0.5xのグラフを書くときに、どういう対策をすることができますか?
対策・・・線を引く命令(line)を使って、xの最大の時と、最小の時のyの値の座標を打ち込んで線を引くなどがあります。
✅ 練習問題 20-2-3
今できる範囲で、y = 0.5xのグラフを描いてみよう。
- キャンバスサイズは400×400px
- 背景色は白(255)
- 線の色は黒(0)
- 両端を x = -10 と x = 10 として計算する
コード
function setup() {
createCanvas(400, 400);
background(255);
}
function draw() {
st = 0;
for (let i = 0; i <= 100; i++) {
stroke(220);
line(st, 0, st, 400);
line(0, st, 400, st);
st += 20;
}
stroke(0);
line(200, 0, 200, 400);
line(0, 200, 400, 200);
line(0, 300, 400, 100);📷 実行結果
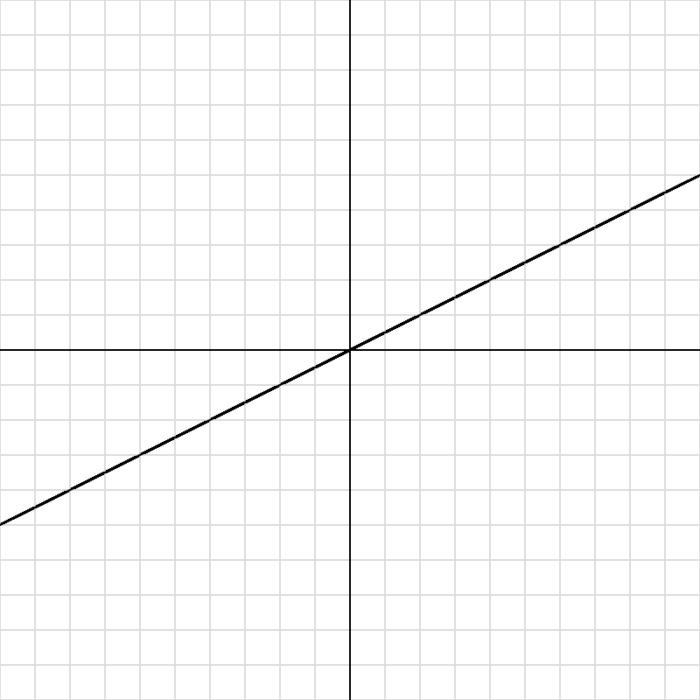
✅ 練習問題 20-2-4
今のままじゃ、グラフ一つ書くのに一苦労です。 計算を簡単にするために、座標変換関数を作ってみよう!
コード
let scale = 20;
function toScreenX(x){ return width/2 + x*scale; }
function toScreenY(y){ return height/2 - y*scale; }
function setup(){
createCanvas(400, 400);
background(255);
stroke(0);
let x1 = -10, y1 = 0.5 * x1;
let x2 = 10, y2 = 0.5 * x2;
line(toScreenX(x1), toScreenY(y1), toScreenX(x2), toScreenY(y2));
}📷 実行結果
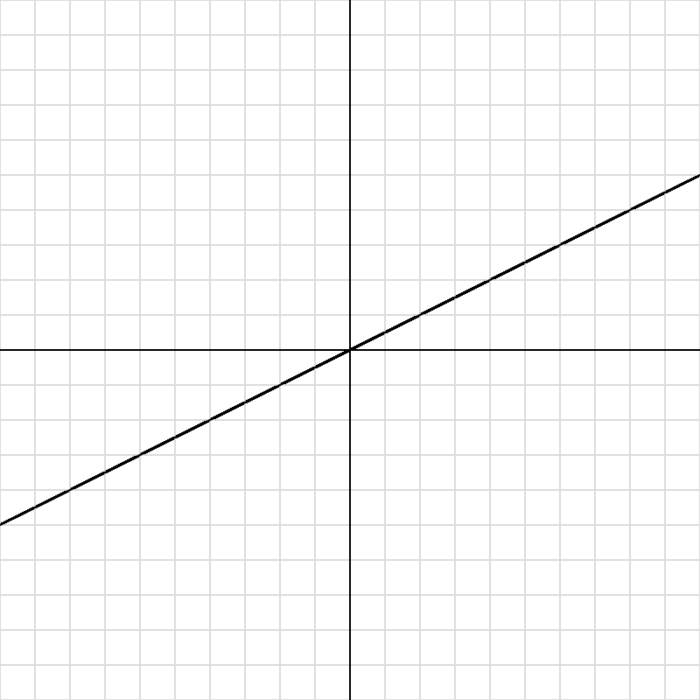
✅ 練習問題 20-2-5
ついさっきのコードを説明できるようにしよう。
説明・・・関数(to Screen)で関数を呼び出し、x座標とy座標を工夫された計算によって数学の授業で使うような感じのものにして、xの変数にマス目の数字を入れると、数学の授業と同じように簡単にグラフを描くことができている。
✅ 練習問題 20-2-6
このコードでは、反比例などの曲線はどう描くのでしょうか?
2点を結ぶ方法では難しいので、別の方法を使って線を引いてみよう。
コード
let scale = 20;
function toScreenX(x){ return width/2 + x*scale; }
function toScreenY(y){ return height/2 - y*scale; }
function setup(){
createCanvas(400, 400);
background(255);
stroke(0);
for (let x = -10; x <= 10; x += 1){
let y = 0.5 * x;
point(toScreenX(x), toScreenY(y));
}
}📷 実行結果
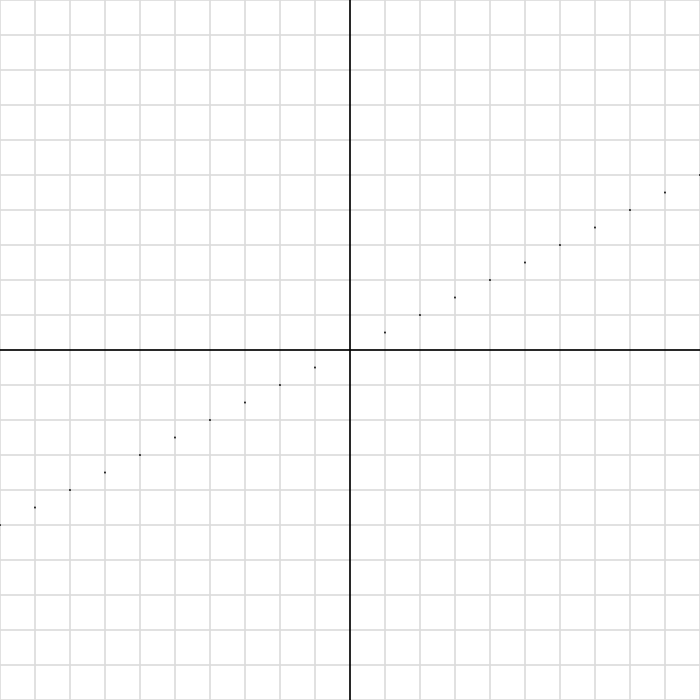
✅ 練習問題 20-2-7
x を 0.05 刻みにして y を計算し、点で描いてみよう。
コード
let scale = 20;
function toScreenX(x){ return width/2 + x*scale; }
function toScreenY(y){ return height/2 - y*scale; }
function setup(){
createCanvas(400, 400);
background(255);
stroke(0);
for (let x = -10; x <= 10; x += 0.05){ ←←←ここのxの増加量を変えるだけ!
let y = 0.5 * x;
point(toScreenX(x), toScreenY(y));
}
}📷 実行結果
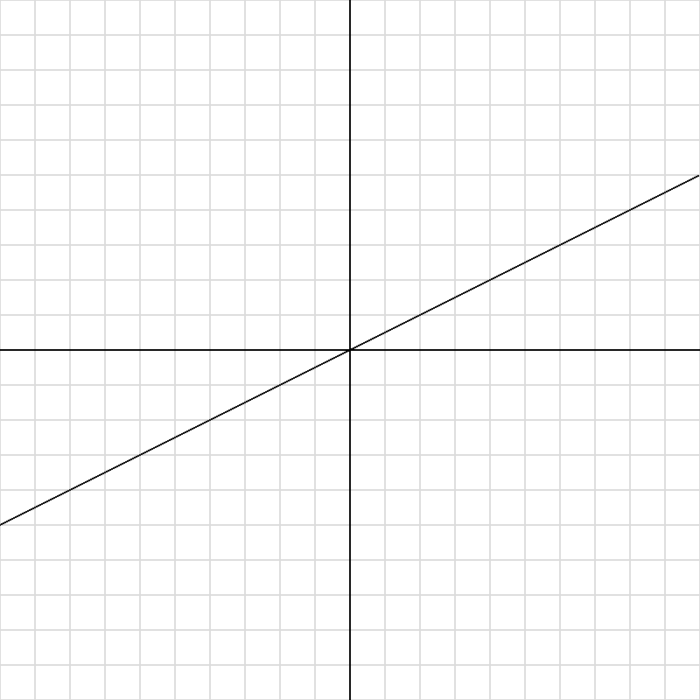
✅ 練習問題 20-2-8
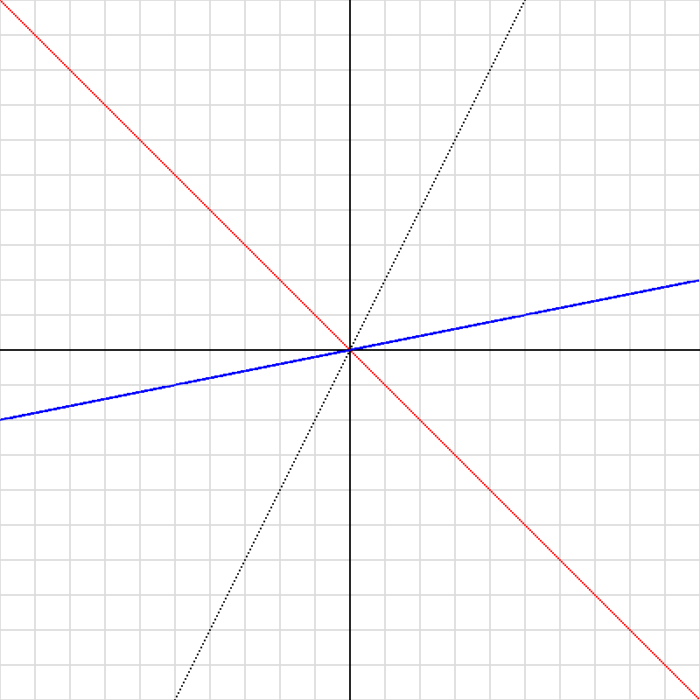
y = 0.5x の係数を変えて、グラフの傾きがどう変わるか確認してみよう。以下の3つを描いてみよう。
- y = 2x を描く(急な傾き)
- y = -x を描く(右下がり)
- y = 0.2x を描く(緩やかな傾き)
コード
let scale = 20;
function toScreenX(x){ return width/2 + x*scale; }
function toScreenY(y){ return height/2 - y*scale; }
function setup(){
createCanvas(400, 400);
background(255);
stroke(0); //黒いグラフ
for (let x = -10; x <= 10; x += 0.05){
let y = 2 * x;
point(toScreenX(x), toScreenY(y));
}
stroke(255, 0, 0); //赤いグラフ
for (let x = -10; x <= 10; x += 0.05){
let y = -x;
point(toScreenX(x), toScreenY(y));
}
stroke(0, 0, 255); //青いグラフ
for (let x = -10; x <= 10; x += 0.05){
let y = 0.2 * x;
point(toScreenX(x), toScreenY(y));
}
}📷 実行結果
✅ 練習問題 20-2-9
for文のステップを0.05に細かくしましたが、0.01や0.001にすればもっと細かくなるのか?
実験する前に予想してみよう!
結果・・・点が一本の線に見えるようになる!
まとめ・感想
・今まで習ってきた「line」による線の引き方では、学校で習っている比例のグラフはかけないことがわかった。
・点を打っていって、段々と細かくしていくと、一本の直線に見えることから、その方法からでも直線を引くことができるとわかった。
・今回のプログラムの最初にある
function toScreenX(x){ return width/2 + xscale; }
function toScreenY(y){ return height/2 – yscale; } による計算がどうなるのかを考えるのが少し難しかった。今回で、改めてプログラムをしっかりと理解することが大切だと思った。